Вся биология ХХ века развивалась под знаком генетики. Ее история начинается с 1885 года, в котором Г. Мендель опубликовал результаты своих восьмилетних наблюдений. Верное слово было сказано, первая модель построена и блестяще подтверждена. Но услышано оно было через 35 лет, через 16 лет после смерти Г. Менделя.
Тому было много причин отметим здесь только одну из них - методологическую. Модель была категоричной и ясной. Она не объясняла всего многообразия явлений наследования, а из-за четкой (по существу - математической) формы не обладала привычной гибкостью расплывчатых объяснений. Наконец, сам метод моделирования был для биологии необычным.
Представляется удивительным, что появление модели, могущей давать точные количественны предсказания в такой загадочной области, как наследование (пусть даже только для некоторых видов и части признаков), не сразу было замечено. В физике, наример, появление кварковой модели (унитарная симметрия элементарных частиц), позволившей предсказать в начале своего развития одну новую элементарную частицу, было принято очень бурно, а ее создатели быстро получили Нобелевскую премию. Но это - физика ХХ века, а речь идет о биологии XIX (если покопаться в истории физики, то и там найдутся подобные грехи).
Как бы поступил современный физик, получи он в свое распоряжение модель, позволяющую описать часть ранее непонятных явлений? Сначала попытался бы распространить на как модно более широкую область. Дойдя до предела применимости, модифицировал бы модель. И так до тех пор, пока дальнейшие улучшения станут невозможными или покажутся неразумными из-за своей громоздкости и потребуется новое понимание (здесь дана, конечно, упрощенная схема). Найденные на этом пути факты послужили бы хорошим подспорьем при поисках новых подходов.
Так, впрочем, поступили и биологи. Но на это ушло много времени. С открытиями Г. Менделя в теорию наследственности пришел новый способ работы, расширивший область применения количественного языка. Биология постепенно созревала для того, чтобы переварить этот переворот, пока, наконец, в 1900 году Г. Де Фриз, Э. Чермак и К. Корренс независимо не переоткрыли законы Менделя.
История науки знает немало трагедий непризнанных первооткрывателей. Судьба Г. Менделя - один из ярких примеров. Он-то наверняка понимал значимость своего открытия. Но трагична и судьба переооткрывателей. Честно пройдя свой путь и совершив великое, они потом узнают, что на вершине уже побывал другой. Единственное, что можно сделать для них, это помнить их имена. Тем, кто повторил открытие Менделя, было легче, 35 лет работы многих исследователей изменили ситуацию, но все же...
У генетики была и своя предыстория. Она связана с именами О. Сарже, Т. Найта и других. Рекомендуем любителям биологии прочитать интересную книгу А. Е. Гайсиновича [27] (она будет полезна и профессионалу).
В заголовке рядом с именем Г. Менделя стоит другое. В. Иоганнсен в 1909 году придал предложенной Г. Менделем модели четкую форму, введя, в частности, термины ``генотип'', ``аллель'' и др. Название книги В. Иоганнсена знаменательно: ``Элементы точного учения о наследственности''. Далее модель совершенствовалась и уточнялась. Велик вклад в этот процесс таких ученых, как В. Бэтсон, Т. Г. Морган и многих других. Мы решили все же включать в название модели только двух авторов первых вариантов, чтобы оно не превратилось в нечто неудобочитаемое.
Молекулярная биология далеко продвинулась в изучении физико-химической природы наследственности, и модели классической генетики относятся уже ко второму типу (феноменологическая модель). Тем не менее, они и по сей день составляют азы современной генетики - с них начинается ее изучение. Но не только азы, еще и основы. Многие положения генетики строятся так: сначала предлагаются простейшие модели , как если бы они точно соответствовали реальности; потом, пользуясь ими как идеальной картиной, формулируются многочисленные уточнения и исключения. Наконец, с некоторого момента эти простые модели могут уже не рассматриваться вовсе или применяться в качестве очень приближенной схемы. По дороге может быть высказано немало ложных (``ограниченно верных'') утверждений, которые уточняются позднее.
Чтобы не быть голословными - два примера. ``В каждой клеточке любого организма данного вида содержится определенное число хромосом''. Это неверно - в некоторых клетках организма утрачена часть хромосом, которым там ``положено быть'', или даже все они (хрестоматийный пример - эритроциты). В других клетках организма ``положенное'' число хромосом удваивается, и еще, и еще... (скажем, в некоторых клетках печени). Обратите внимание: мы отрицали утверждение, пользуясь им самим, применяя введенное в нем понятие ``определенное для данного вида число хромосом'' для описания контрпримера. Еще один пример: ``У диплоидного организма имеется по два гена каждого типа, причем эти гены занимают одинаковые локусы (места) в гомологичных хромосомах''. Это тоже не соответствует истине. Некоторых генов в одной из хромосом может не быть совсем (нехватки), а какие-то могут содержаться в нескольких экземплярах (дупликации). Мы специально не указываем источники цитат, чтобы не создавать ложного впечатления дискуссии. Авторы приведенных отрывков прекрасно понимают условность сделанных утверждений и демонстрируют это в дальнейшем развитии текстов.
Такой способ излагать научную теорию: сначала понятия вводятся на простых примерах, а потом постепенно уточняются - не единственно возможный. Его порою ошибочно считают некорректным, хотя он широко распространен и при правильном употреблении приводит к успеху. Этот способ иногда называют развертыванием, а еще - восхождением от абстрактного к конкретному. Начальные простые и ``неправильные'' модели здесь необходимы.
Попытаемся изложить основные идеи моделей классической генетики, вообще не обращаясь к клеткам организма (соматическим). Будем следовать известному афоризму: ``Курица - это всего лишь способ, каким яйцо создает другое яйцо''.
Первое положение модели: наследственные свойства организмов определяются набором дискретных единиц - генов, полученных им от родителей. С этой точки зрения генотип - множество генов.
Но не просто множество. Важную роль играют дополнительные структуры. Второй вариант определения: генотип - множество генов, распределенных по хромосомам. И снова, конечно, неполно и неточно.
Для каждого вида существует конечный набор типов хромосом и определено
правило, указывающее, сколько (в норме) хромосом каждого типа может быть в
генотипе. Вариации, допускаемые этим правилом, обычно очень незначительны. У
человека, например, 24 типа хромосом (22 типа аутосом и 2 типа половых
хромосом ![]() и
и ![]() . В норме генотип должен содержать 22 пары аутосом (от каждого
родителя по одной аутосоме каждого типа) и пару половых хромосом : XX или
XY. Любое отклонение от этого правила приводит к тяжелым заболеваниям.
. В норме генотип должен содержать 22 пары аутосом (от каждого
родителя по одной аутосоме каждого типа) и пару половых хромосом : XX или
XY. Любое отклонение от этого правила приводит к тяжелым заболеваниям.
Так же, как набор хромосом в генотипе, не может быть произвольной последовательность генов в хромосоме. С этой точки зрения хромосома представляет собой последовательность локусов (локус по латыни означает место). Для каждого локуса определено множество форм (состояний) гена - аллелей. Итак, для каждого типа хромосомы задана последовательность локусов (так сказать, ``типов'' генов), для каждого локуса - набор аллелей (``состояний заполнения'') этого места.
Хромосома - как бусы, локус - место бусинки (ее номер), аллель - сама бусинка. Недостаток этой аналогии - легкость, с которой одну и ту же бусинку можно поместить на разные места. Аллели же, напротив, довольно четко прикреплены к локусам.
В модели Менделя-Иоганнсена последовательность локусов принимаем фиксированной и все различия в хромосомах относим за счет различных аллелей. Напомним, что рассматривается модель, которая относится сейчас в науке не к первому типу, а ко второму - феноменологическая модель. Реальность не просто сложнее (она всегда сложнее), а отличается от модели в своих существенных свойствах, выделенных и освоенных наукой. То, что гена в хромосоме может просто не быть (нехватка), легко формализуется добавлением ``пустого'' аллеля. Дупликации (удвоения) тоже можно учесть такис способом, называя аллелем пару (форма гена, число повторов). Дальнейшее усложнение связано с тем, что есть прыгающие генетические элементы - от предположения о фиксированности последовательности локусов приходится отказаться [108,120]. Если бы прыжки были редки, то их можно было бы учесть и в этой модели, вводя новые локусы и приравнивая прыжок к мутации в этих локусах, но реальная частота прыжков делает такое усложнение бессмысленным.
Расшатывание классической модели завершается молекулярной биологией, которая, хотя и прояснила физико-химический механизм наследственности, но поставила проблему: что считать геном классической модели? Какая часть гигантской молекулы ДНК соответствует этому понятию? На такой вопрос можно давать разные ответы и из них нельзя сделать однозначный выбор - не потому, что не хватает информации, а потому, что классический ген - элемент феноменологической модели, который может интерпретироваться различными способами.
Вот некоторые дискретные единицы, которые могут быть выделены (следуем работе [85]):
``Кодон - компактная, линейно упорядоченная совокупность азотистых оснований (три основания - примеч. Авт.), кодирующая включение отдельной аминокислоты в биосинтез белка. ...
Цистрон - компактная, линейно упорядоченная совокупность кодонов, определяющая первичную структуру отдельной молекулы белка. ...
Оперон - компактная, линейно упорядоченная совокупность цистронов, определяющая координированный синтез группы белков. ...
Репликон - компактная, линейно упорядоченная совокупность оперонов и других сообщений низших рангов, принадлежащая одному материальному носителю и реплицирующаяся (удваивающаяся при редупликации - примеч. авт.) как целое.
Сегрегон - (группа сцепления) ...''
Вряд ли следует считать геном кодон, но все остальные единицы - реальные претенденты на звание гена. Это довольно давняя классификация (1968 г.). Сейчас ее можно было бы построить по-другому, используя новые достижения, но суть от этого не изменится. Существуют сильно отличающиеся по характерной величине участки ДНК, равноправно претендующие на звание гена (группа сцепления - сегрегон может содержать тысячи цистронов, кодирующих отдельные молекулы белка). Можно и договориться: пусть, например, ген есть цистрон. Но это не решение вопроса, а, скорее, его маскировка.
Правильнее будет так: при использовании моделей генетики допустимо называть геном разные объекты. Важны два условия - формальное и содержательное. Формальное: в ходе решения одной задачи смысл термина не должен меняться (профессионал выполняет такое условие автоматически). Содержательное: в течение интересующих нас времен ген должен передаваться от родителей потомкам в большинстве случаев без изменений.
Простейшую модель полового размножения рассмотрим только для диплоидных организмов, т.е. тех,
генотип которых содержит по две хромосомы каждого типа. Есть и тут
исключение. У раздельнополых организмов половые хромосомы могут не
образовывать однотипной пары: у мужчин - XY, у самцов некоторых видов число
хромосом вообще нечетно, половая не имеет пары - ![]() . Бывает и наоборот, у
отдельных видов самцы имеют все хромосомы однотипными парами, а самки - XY или
. Бывает и наоборот, у
отдельных видов самцы имеют все хромосомы однотипными парами, а самки - XY или
![]() . Диплоидные особи производят гаметы - клетки, содержащие только по одной
хромосоме каждого типа. Если половые хромосомы особи неоднотипны, то в
случае XY половина гамет получает
. Диплоидные особи производят гаметы - клетки, содержащие только по одной
хромосоме каждого типа. Если половые хромосомы особи неоднотипны, то в
случае XY половина гамет получает ![]() , а половина -
, а половина - ![]() ; для
; для ![]() аналогично: половина
гамет несет
аналогично: половина
гамет несет ![]() , а половина не несет половой хромосомы.
, а половина не несет половой хромосомы.
Гаметы различных особей (при раздельнополом размножении разнополых) сливаются, образуя диплоидную клетку (зиготу), дающую начало новому организму. Первый вопрос: что происходит при половом размножении в одном аутосомном локусе (т.е. локусе не половой хромосомы)? Напрашивается ответ: если родительская особь несет в одном локусе только один аллель (гомозиготна), то этот аллель попадает во все гаметы и, таким образом, все ее потомки в первом поколении могут иметь в генотипе этот аллель. Если же особь несет в этом локусе два аллеля (гетерозиготна): один - в одной хромосоме данного типа, а второй - в другой, то половина гамет будет нести первый, а половина - второй аллель и, соответственно, половина потомков в первом поколении получат от этого родителя первый аллель, а другая половина - второй. Такое правило распределения аллелей в потомстве составляет главное содержание первого закона Менделя. Обычно он формулируется несколько по-другому и представляет собой ближайшее следствие описанного правила.
Г. Мендель исследовал расщепление гибридов гороха. Гибриды несли в
одном из локусов два различных аллеля - были гетерозиготны. Один
из этих аллелей (A![]() был доминантным, т.е. фенотипически
гетерозиготы были неотличимы от растений, гомозиготных по этому
аллелю. Другой, рецессивный аллель (a
был доминантным, т.е. фенотипически
гетерозиготы были неотличимы от растений, гомозиготных по этому
аллелю. Другой, рецессивный аллель (a![]() проявлялся только в
гомозиготном состоянии. При скрещивании гетерозигот
проявлялся только в
гомозиготном состоянии. При скрещивании гетерозигот ![]() гаметы
гаметы ![]() и (A) производятся в одинаковом количестве.
Предполагается, что они комбинируются случайно, поэтому зиготы
образуются в следующем соотношении:
и (A) производятся в одинаковом количестве.
Предполагается, что они комбинируются случайно, поэтому зиготы
образуются в следующем соотношении:
![]() . Из-за
доминантности
. Из-за
доминантности ![]() фенотипы aA и AA не различаются,
следовательно, расщепление фенотипов происходит так: 3(Aa или AA)
+ 1(aa) - знаменитое 3:1. Это и есть первый закон Менделя в его
обычной формулировке. Он имеет статистический характер -
справедлив в среднем.
фенотипы aA и AA не различаются,
следовательно, расщепление фенотипов происходит так: 3(Aa или AA)
+ 1(aa) - знаменитое 3:1. Это и есть первый закон Менделя в его
обычной формулировке. Он имеет статистический характер -
справедлив в среднем.
Второй закон Менделя относится к паре локусов. Если родительская особь гетерозиготна по двум локусам, то простейшее предположение, которое можно высказать о продуцируемых гаметах, состоит в независимости представленного в гамете аллеля первого локуса от того, какой аллель у нее во втором. Предполагая также, что гаметы комбинируются случайно, и получаем второй закон Менделя. Обычно его формулируют как независимость расщепления в разных локусах.
Закон этот неприменим, однако, к локусам из одной хромосомы. Расхождение генов по гаметам не является независимым. Чем ближе локусы - тем сильнее зависимость. Близкие локусы объединяются в ``группы сцепления''.
Первый закон выглядит более убедительно, поэтому неожиданным оказалось открытие генов, которые его нарушают. Высказано и обосновано предположение, что в некоторых случаях это нарушение вызывается геном (несколькими генами), который так воздействует на своего ``партнера'', расположенного в том же локусе парной хромосомы (``оскорбляет'' его), что партнер, попав в гамету, ``кончает жизнь самоубийством'', нарушая ее функционирование. Что это за воздействие? Вопрос сложный. Легко понять, почему в популяции не может быть очень большим процент особей, несущих в данном локусе таких ``генов-грубиянов''. Особи, гомозиготные по ним, оставляют очень мало потомства, так как после взаимных ``оскорблений'' почти все гаметы нежизнеспособны. Исходя из этого нетрудно оценить, в каком проценте генотипов эти гены будут присутствовать, их около 50% . В природных же популяциях дрозофилы, где были обнаружены такие гены, их раз в десять меньше. Почему? Появление ``грубиянов'' создает новую генетическую среду, в которой получают преимущество гены ``нечувствительные к оскорблениям''. Последние не мешают плодовитости особей, гомозиготных по ним, и потому имеют преимущество и перед ``грубиянами''. В результате устанавливается равновесие, в котором грубиянов'' немного.
Наше изложение кратко и приблизительно. Детали можно найти в интересной статье [58]. В частности, ``гены-грубияны'' у дрозофилы, описанные в этой статье, нарушают обычный сперматогенез у самцов и не вмешиваются в образование гамет у самок.
Эффекты такого типа объединяются под названием ``мейотический драйв''. Они обнаружены у многих видов: комаров, мышей, некоторых растений и др. Наличие и распространение мейотического драйва показывает несостоятельность примитивных аргументов, объясняющих половое размножение и первый закон Менделя выгодностью высоких темпов эволюции. Если ген, неблагоприятный с какой-либо точки зрения, может внедриться и с этих позиций ухудшить систему, то он внедрится и ухудшит, ничего не поделаешь.
Каких изменений в моделях ``отбор по признаку'' может потребовать генетика? Вот знаменитый пример из генетики человека. Пусть люди, населяющие некоторую территорию, могут быть носителями одного из трех фенотипов (остальными различиями пренебрегаем): больные серповидноклеточной анемией, не доживающие до совершеннолетия; люди, не страдающие анемией и легко переносящие малярию (либо не болеющие ей вовсе); не страдающие анемией, но тяжело переносящие малярию. Пусть также эти свойства предопределены от рождения. Если на рассматриваемой территории малярия - частое заболевание, то с точки зрения простейших моделей ``отбор по признаку'' должен, казалось бы, оставлять только один фенотип: ни малярии, ни анемии. Однако, увы, соответствующий генотип гетерозиготен.
Исследования показали, что описанной ситуации хорошо подходит однолокусная
модель. В этом локусе различаются два аллеля - нормальный ![]() и мутантный
и мутантный ![]() . Ген
(аллель)
. Ген
(аллель) ![]() вызывает в гомозиготном состоянии изменения гемоглобина и
искажения формы эритроцитов. Организм, получивший
вызывает в гомозиготном состоянии изменения гемоглобина и
искажения формы эритроцитов. Организм, получивший ![]() от обоих родителей
(SS), гибнет во младенчестве. Если генотип полностью нормален (NN), то организм
легко заболевает малярией и тяжело ее переносит. Наконец, носители
гетерозиготного генотипа (NS) устойчивы к малярии и не гибнут от анемии. В итоге
сохраняются все три фенотипа - преимущество гетерозигот компенсирует гибель
(SS) и потому в популяции много носителей тех генов, которые в гомозиготном
состоянии вредны, даже смертельно вредны - летальны.
от обоих родителей
(SS), гибнет во младенчестве. Если генотип полностью нормален (NN), то организм
легко заболевает малярией и тяжело ее переносит. Наконец, носители
гетерозиготного генотипа (NS) устойчивы к малярии и не гибнут от анемии. В итоге
сохраняются все три фенотипа - преимущество гетерозигот компенсирует гибель
(SS) и потому в популяции много носителей тех генов, которые в гомозиготном
состоянии вредны, даже смертельно вредны - летальны.
Проведем элементарное исследование баланса генов в одном локусе. Пусть
различаются два аллеля ![]() и
и![]() и соответственно три генотипа: NN, NS, SS (обозначения
сохраним те же, что и для серповидноклеточной анемии).
и соответственно три генотипа: NN, NS, SS (обозначения
сохраним те же, что и для серповидноклеточной анемии).
В построении модели будут участвовать такие величины. Численности зигот
сразу после слияния гамет для различных генотипов:
![]() . Численности гамет, слившихся в эти зиготы:
. Численности гамет, слившихся в эти зиготы:
предполагаем комбинирование гамет случайным, поэтому отношение
![]() должно совпадать с
должно совпадать с
![]() .
Это в точности означает, что
.
Это в точности означает, что
где ![]() - число, общее для всех
- число, общее для всех ![]() . Его нетрудно выразить через
. Его нетрудно выразить через
![]() , однако далее оно нам не понадобится.
, однако далее оно нам не понадобится.
Предполагаются заданными относительные жизнеспособности зигот:
![]() Что это за числа? Их
вводят, исходя из представлений о разделении факторов,
определяемых генотипом, и прочих. Аналогичная конструкция
появляется в предыдущей главе при разборе простейших моделей
отбора по признаку. Жизнеспособность оценивается по участию в
создании нового поколения. Для такого участия из новенькой зиготы
должен развиться организм, дожить до размножения и произвести
гаметы, входящие во вновь образующиеся зиготы.
Что это за числа? Их
вводят, исходя из представлений о разделении факторов,
определяемых генотипом, и прочих. Аналогичная конструкция
появляется в предыдущей главе при разборе простейших моделей
отбора по признаку. Жизнеспособность оценивается по участию в
создании нового поколения. Для такого участия из новенькой зиготы
должен развиться организм, дожить до размножения и произвести
гаметы, входящие во вновь образующиеся зиготы.
Имеем только что образовавшуюся зиготу NN, NS или
SS. Предполагается, что в среднем на одну такую зиготу с
данным генотипом придется
![]() гамет,
вошедших в состав вновь образовавшихся зигот следующего поколения.
Множитель
гамет,
вошедших в состав вновь образовавшихся зигот следующего поколения.
Множитель ![]() зависит от большого числа факторов, а зависимость от
генотипа сконцентрирована в множителях
зависит от большого числа факторов, а зависимость от
генотипа сконцентрирована в множителях ![]() . Основное упрощающее
предположение состоит в том, что возможно такое разложение на
множители:
. Основное упрощающее
предположение состоит в том, что возможно такое разложение на
множители: ![]() зависит от чего угодно, но не от генотипа, а
зависит от чего угодно, но не от генотипа, а ![]() -
только от генотипа.
-
только от генотипа.
Зададимся вопросом: пусть известны численности гамет
![]() образовавших зиготы данного поколения; каковы тогда будут численности гамет
образовавших зиготы данного поколения; каковы тогда будут численности гамет
![]() образовавших зиготы следующего поколения? (мотив:
``Курица - всего лишь способ...''). штрих означает переход к следующему
поколению. Предполагая выполненным первый закон Менделя, сразу получаем
(упражнение);
образовавших зиготы следующего поколения? (мотив:
``Курица - всего лишь способ...''). штрих означает переход к следующему
поколению. Предполагая выполненным первый закон Менделя, сразу получаем
(упражнение);
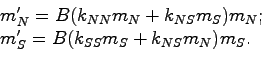
здесь ![]() - некоторое число, в которое вошли множителями
и
- некоторое число, в которое вошли множителями
и ![]() Б и неизвестное нам
Б и неизвестное нам ![]() . Далее важно только, что
. Далее важно только, что ![]() и
одинаково для
и
одинаково для ![]() .
.
Получена модель генетического баланса в ее простейшей
форме. В ней можно выделить коэффициенты размножения для ![]() и
и ![]() - отношения
- отношения
![]() . Если в равновесии есть и
. Если в равновесии есть и ![]() и
и ![]() , то их коэффициенты
размножения должны быть при этом равны единице. Исследовать это
условие, однако, нельзя - неизвестны множители
, то их коэффициенты
размножения должны быть при этом равны единице. Исследовать это
условие, однако, нельзя - неизвестны множители ![]() . Можно, тем не
менее, записать для коэффициентов размножения условие их равенства
друг другу, в котором
. Можно, тем не
менее, записать для коэффициентов размножения условие их равенства
друг другу, в котором ![]() сократится:
сократится:
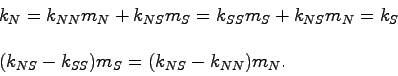
Если величины
![]() имеют разные
знаки, то равновесие с положительными значениями обеих величин
имеют разные
знаки, то равновесие с положительными значениями обеих величин
![]() невозможно. Это понятно: в таком случае
гетерозиготы выживают хуже, чем одна из гомозигот, но лучше, чем
другая и один аллель (понятно, какой) вытесняется другим.
невозможно. Это понятно: в таком случае
гетерозиготы выживают хуже, чем одна из гомозигот, но лучше, чем
другая и один аллель (понятно, какой) вытесняется другим.
Положительное равновесие (баланс)
существует в двух случаях: и когда гетерозиготы более приспособлены, чем обе
гомозиготы, и когда они менее приспособлены. Последнее кажется странным,
однако можно убедиться, что при
![]() равновесие неустойчиво: если
равновесие неустойчиво: если
то соответствующий коэффициент размножения ![]() также больше:
также больше: ![]() или
или
(упражнение). Аналогично и для обратного неравенства. Поэтому со временем
любое уклонение от равновесного отношения ![]() будет возрастать.
Это приведет к тому, что через достаточно большое время в системе останется
только один аллель - тот, в пользу которого вначале нарушено равновесное
отношение
будет возрастать.
Это приведет к тому, что через достаточно большое время в системе останется
только один аллель - тот, в пользу которого вначале нарушено равновесное
отношение ![]() . Победитель зависит от начальных условий.
. Победитель зависит от начальных условий.
Простейшая модель генетического баланса дает важный урок. Коэффициент размножения, вводившийся раньше для особей, используется только для описания динамики генов (аллелей). Размножающаяся единица стала мельче. Также должен стать мельче элемент, к которому относится представление о выгоде, оптимальности, пользе.
В предыдущей главе рассматривалась схема эксперимента по внедрению, наполняющая смыслом представления о выгоде, пользе и порождающая принципы оптимальности. Группа особей малой, но достаточной для размножения численности внедряется в биогеоценоз и либо вымирает, либо успешно размножается. Все внедряемые особи должны наследуемо (со всеми будущими потомками, которые появятся в ходе эксперимента) принадлежать одной клеточке (точке) номенклатуры изменчивости. Можно даже сказать так: внедряется эта клеточка (точка), а особи ее несут.
С точки зрения балансовых моделей генетики как целое воспроизводится ген (аллель), а не особь как генотип, поэтому рассматривать следует внедрение аллеля. Аллель внедряется в составе генотипа особи, особь в составе небольшой группы. Теперь не исключено, что особи внедренной группы будут скрещиваться с другими, в нее не входящими. Рассматривается судьба аллеля: внедрится - не внедрится, выживет - не выживет.
В балансовых моделях так же, как в классических, возникают принципы совместной оптимальности - сооптимальность аллелей. Каждый из устойчиво сосуществующих аллелей оптимален на фоне остальных. Был предложен специальный термин ``геноценоз'' (см., например, вступительную статью А. С. Антонова к сборнику [120], c.7), который подчеркивает особый взгляд на систему взаимодействующих генов как на биоценоз и, можно добавить, на биоценоз как на систему взаимодействующих генов. Возникает иерархическая лестница на ступеньку длиннее, чем в классических моделях: из аллелей слагаются генотипы особей, из особей - популяции, из популяции - биоценозы.
Конечно, область применимости для представлений о сооптимальности аллелей значительно шире, чем для простых балансовых моделей. В частности, не требуется никаких гипотез о разделении факторов (как вы помните, с помощью таких гипотез достигалось разделение генетики и экологии при построении простейшей балансовой модели). Эти представления о сооптимальности базируются на схеме экспериментов по внедрению.
В истории балансовых моделей произошел один казус, который сильно
и, как нам кажется, не очень удачно повлиял на общие представления
о динамике отбора. Исследуя простейший класс балансовых моделей,
Р. Фишер доказал, что устанавливается такое равновесие аллелей,
которое обеспечивает максимум средней приспособленности организма
в популяции. Приспособленности измеряются с помощью коэффициентов
![]() или их аналогов - формальные детали можно найти в любом
подробном руководстве (например, в [91]).
или их аналогов - формальные детали можно найти в любом
подробном руководстве (например, в [91]).
Этот факт произвел в момент своего появления большое впечатление и был назван основной теоремой о естественном отборе. Его часто трактуют так: отбор-де пренебрегает выгодой для отдельной особи, его заботит популяция в целом.
Увы, теорема Фишера не выполняется уже для чуть более сложных моделей. Она тесно связана с гипотезой о разделении факторов. Сейчас известно, когда из более сложных и общих эколого-генетических моделей могут быть получены уравнения Фишера. Оказывается, для этого требуется, чтобы отличия между носителями различных генотипов были малы. Тогда в первом приближении по этой малости и получаем уравнения Фишера, а с ними его теорему (вспомните модели типа 3 - что-то считаем очень большим или очень малым).
Принципы сооптимальности, восходящие по своей идее к Дж. Б. С. Холдейну, имеют значительно более общую эколого-генетическую природу. Это - принципы оптимальности аллелей, слагающих генетический компонент системы (биогеоценоза), на фоне всей этой системы. Поэтому они относятся сразу к каждому отдельному аллелю (который должен быть точкой единичного максимума коэффициента размножения на пространстве возможностей) и к системе, которая определяет коэффициент размножения, к биогеоценозу в целом.
Есть две возможные причины для нарушения сооптимальности. Первая - высокий темп изменчивости, тогда теряют смысл представления о передаче аллелей из поколения в поколение. Вторая - отсутствие устойчивых равновесий, наличие более сложной динамики генетического состава, но в этом случае сооптимальность будет выполняться в среднем за большее время.
Существует важное различие между балансовыми и классическими моделями. На первый взгляд оно кажется техническим, но это не так. Пусть в популяции присутствует небольшое количество носителей доминантного аллеля и они все плохо приспособлены - дают мало выживающего потомства (так как аллель доминантен и несущие его гетерозиготы мало отличаются от гомозигот). Тогда количество этих носителей уменьшается в геометрической прогрессии - как и для особей в классических моделях.
А вот если аллель рецессивен и плохо приспособлены - гибнут, не размножаются
и т. п. гомозиготные по нему особи, тогда все по-другому. Число гомозигот
можно оценить как ![]() , где
, где ![]() - доля аллеля в популяции,
- доля аллеля в популяции, ![]() -
полная численность популяции. Скорость убыли
-
полная численность популяции. Скорость убыли ![]() будет пропорциональна
будет пропорциональна
![]() , поэтому со временем
, поэтому со временем ![]() будет уменьшаться не в геометрической
прогрессии, а значительно медленнее - как
будет уменьшаться не в геометрической
прогрессии, а значительно медленнее - как ![]() . Здесь отличие от классической
модели.
. Здесь отличие от классической
модели.
Рецессивность существенно увеличивает время жизни внедренного аллеля и даже меняет закон его вымирания, когда он ``не помогает'' своим гетерозиготам и ``вреден'' (даже смертельно) своим гомозиготам.
Отсюда насыщенность популяций рецессивными ``умеренно вредными'' мутациями, наличие достаточного времени для того, чтобы они были испытаны в разных сочетаниях и, возможно, образовали бы уже ``полезные'' комбинации. Все это может считаться благом с точки зрения человека - сторонника прогресса. Тем не менее, не очень ясно, играл ли в установлении этого механизма какую-нибудь роль отбор и связанные с ним принципы оптимальности, кроме банальной: рецессивные аллели сохраняются, потому что они рецессивны и долго сохраняются.
Описаны еще такие интересные эффекты, как управление доминантностью, когда гетерозиготный организм ``включает в работу'' те аллели, которые способствуют его развитию и выживанию в данных условиях. Интереснейший вопрос: как могла сложиться в ходе эволюции эта система управления, где она локализуется и наследуется?
З а м е ч а н и е. в главе ``Модель Дарвина'' мы определили генотип как то, что получено от рождения, - очень широко. В данной главе генотип - система генов, это узко. Для ряда целей может оказаться удобным разделить подходы и ввести для системы генов термин ``геном''.